Strahlungsmessungen⚓︎

Messung der Temperaturstrahlung bei U-CUBE (Dr. Milan Dlabal, 20.7.2018)⚓︎

Bei der physikalischen Beurteilung der in einem Gebäudeablaufenden Wärmeübertragung spielt der Strahlungsaustausch eine wichtige Rolle. Insbesondere unter Aspekten der thermischen Behaglichkeit nach DINEN 7730 kommt der Wärmestrahlung eine besondere Bedeutung bei.

Nach ISO 7243, ISO 7726, DINEN 27726 und DIN 33403 kann dieStrahlungstemperatur entweder aus der Kenntnis der Oberflächentemperaturen bestimmt werden oder aber mit dem Globethermometer gemessenwerden. Insbesondere ein Globethermometer ist aber wegen der enormen Trägheit (20 bis 30 Minuten) nicht für Echtzeitmessungen der Strahlungstemperatur geeignet. Inden Messkuben des U-CUBE Projekts wird die Wärmestrahlung durch direkte Strahlungssensoren und durch Messung der Oberflächentemperaturen der Wände gemessen.

In der Regel stellt das Wärmeübertragungssystem (Heizung) die einzige Wärmequelledar. An sonnigen Heiztagen kann die solare Erwärmung einer oder mehrerer Außenwände oder des Daches zu einem zusätzlichen Wärmeeintrag in die massiv gebauten CUBES führen. Hier soll nun zunächst die thermodynamische Situation der Wärmestrahlung im Inneren eines U-CUBE's beschrieben werden.

In der würfelförmigen Geometrie der Kuben haben wir 7 Körperoberflächen zu betrachten, die miteinander im Strahlungsaustausch stehen: Die Heizfläche (A1), die hier zunächst als Plattenheizkörper angenommen wird, die Wand hinter dem Heizkörper (A2), die gegenüber liegende Wand (A3), den Boden (A4), die Decke (A5) und die beiden angrenzenden Seitenwände (A6 und A7).

Zunächst wird die Einstrahlzahlenmatrix für diese Konfiguration berechnet. Für die Wände gelten zwei verschiedene Situationen im Würfel: senkrechte Quadrate mit gemeinsamer Kante sowie koaxiale, parallele Quadrate.Für senkrechte Quadrate gleicher Größe mit einer gemeinsamen Kante (vergl. J. R. Howell: http://www.engr.uky.edu/rtl/Catalog/) ist

\[ F_{34}= F_{43}= \frac{1}{\pi} \left( 2 \arctan 1 - \sqrt{2 \arctan \left( \frac{1}{\sqrt{2}} \right) } + \frac{1}{4} \ln \frac{4}{3} + \frac{1}{2} \ln \frac{3}{4} \right) = 0,2 \]

Für die gegenüber liegende Fläche im Würfel ergibt sich nach der Summationsregel eine Einstrahlzahl von ebenfalls 0,2.

Zum Vergleich (ebend.):

\[ F_{42} = F_{54} = \frac{2}{\pi} \left( \frac{1}{2} \ln \frac{4}{3} + \sqrt{2 \arctan \frac{1}{\sqrt{2}}} + \sqrt{2 \arctan \frac{1}{\sqrt{2}}} - 2 \arctan 1 \right) = 0,2 \]

Jede Innenwand im Würfel trägt genau zu einem Sechstel zum Strahlungsaustausch bei.

In der folgenden Betrachtung sei ohne Beschränkung der Allgemeinheit die Heizfläche wandmittig montiertund ebenfalls quadratisch. Die Einstrahlzahl der Heizung auf die gegenüberliegende Wand ergibt sich dann wiederum aus der Formel für die koaxialen, parallelen Quadrate. Nun muss allerdings die Größe der Heizfläche in Relation zur Wand berücksichtigt werden. Für diese Rechnung soll die Heizung eine Kantenlänge von 0,6m haben. Die Innenseiten der Wände bei U-CUBE sind 2,7m lang. Daraus ergibt sich eine Einstrahlzahl F₁₃ = 0,2372.

Die Einstrahlzahl F₃₁ ergibt sich aus der Reziprozitätsbeziehung:

\[ F_{31}=frac(F_{31}*A1)(A3)=0,0117 \]

Die Einstrahlzahl F₃₂ der Wand um die Heizung wird von der gegenüber liegenden Wand nach der Summenregel ermittelt:

\[ F_{32}=0,2-F_{31}=0,1883 \]

Die Einstrahlzahl F₂₃ in Gegenrichtung folgt wiederum durch die Reziprozitätsbeziehung:

\[ F_{23}==\frac{F_{32} \cdot A_3}{A_3-A_1}=0,19808 \]

Durch die Symmetrie der Anordnung können die Einstrahlzahlen zwischen der Heizung, der Rückwand und den Seitenwänden leicht ermittelt werden.

Es gilt:

\[ F*{14}=F*{15}=F*{16}=F*{17}=\frac{1-F*{13}}{4}=0,1907 \\\ F*{41}=F*{51}=F*{61}=F*{71}=\frac{F*{14} \cdot A_1}{A_4}=0,009417 \]

Analog gilt:

\[ F*{24}=F*{25}=F*{26}=F*{27}=\frac{1-F*{23}}{4}=0,20048 \\\ F*{14}=F*{15}=F*{16}=F*{17}=\frac{1-F*{13}}{4}=0,1907 \]

Die Einstrahlzahlenmatrix Φ der Konfiguration hat die folgende Form:

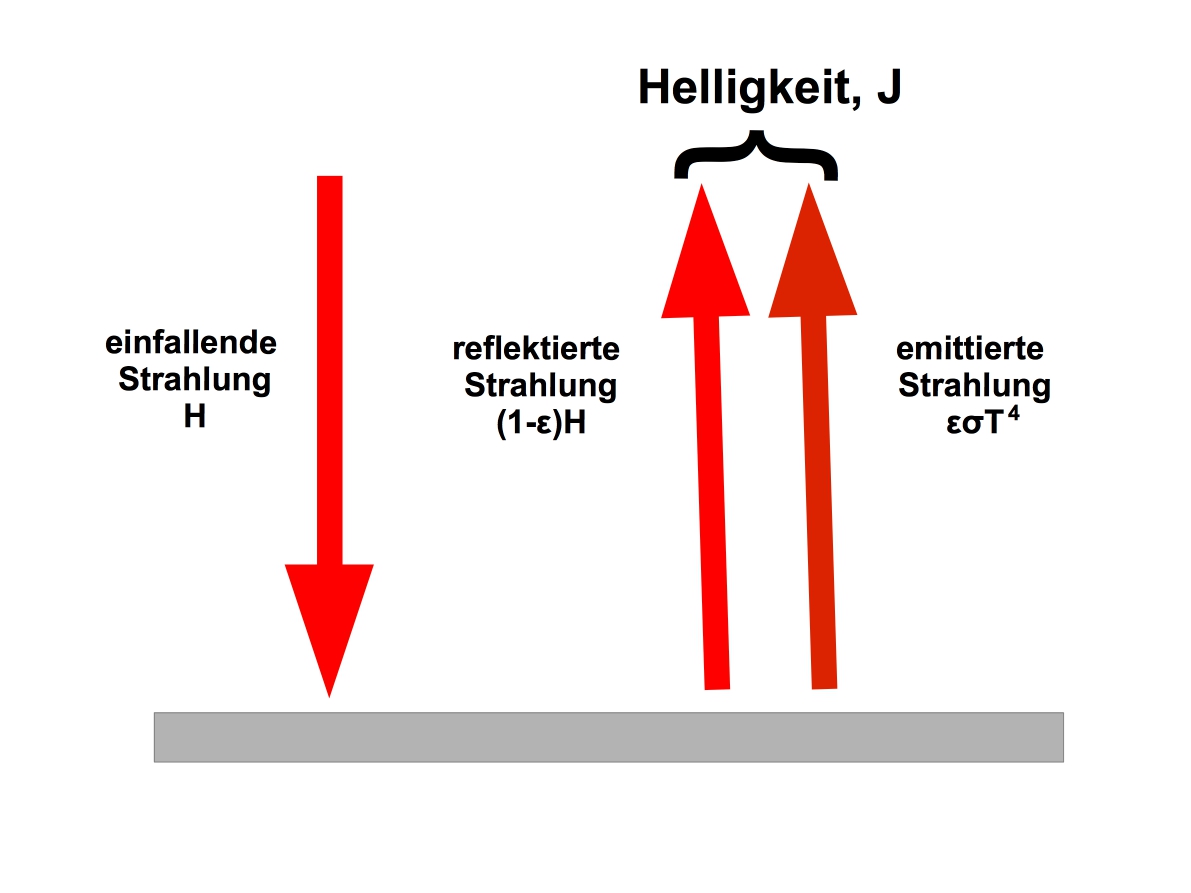
Die Hauptdiagonalelemente verschwinden vollständig, da sich die ebenen Teilflächen nicht selbst sehen. F₁₂ und F₂₁ sind ebenfalls Null, da die Heizung nicht die Wand um sie herum sieht und umgekehrt. Die Berechnung der Wärmestromdichte der Heizung geschieht durch eine Analyse der thermischen Helligkeiten der grauen, opaken Oberflächen mit bekannten Oberflächentemperaturen. Dabei ist die Helligkeit (J (radiosity) in W/m²) die emittierte Strahlung plus der reflektierte Anteil der auftreffenden Strahlung.

Somit gilt für jede Oberfläche:

Im Folgenden werden wiederum ohne Beschränkung der Allgemeinheit alle Emissivitäten gleich gesetzt:

\[ ε_{i} = ε \]

Damit lassen sich 7 lineare Gleichungen aufstellen. Das sei exemplarisch für J₁ gezeigt:

\[ J_1 + \frac{1-ε}{ε} \left[ F_{12} (J_1 - J_2) + F_{13} (J_1 - J_3) + F_{14} (J_1 - J_4) + F_{15} (J_1 - J_5) + F_{16} (J_1 - J_6) + F_{17} (J_1 - J_7) \right] = ε \cdot T_{14} \]

Multiplikation mit ε und Umordnen nach den Helligkeiten führt zu einer einfacheren Gleichung:

\[ J_1 - \left(1-ε\right) \left[ F_{12} J_2 + F_{13} J_3 + F_{14} J_4 + F_{15} J_5 + F_{16} J_6 + F_{17} J_7 \right] = ε \cdot T_{14} \]

Das lineare Gleichungssystem lässt sich in Matrixschreibweise kompakt darstellen:

\[ \begin{align*} & \left[ \begin{array}{ccccccc} 1 - (1 - \epsilon)F_{12} & -(1 - \epsilon)F_{13} & -(1 - \epsilon)F_{14} & -(1 - \epsilon)F_{15} & -(1 - \epsilon)F_{16} & -(1 - \epsilon)F_{17} \\ -(1 - \epsilon)F_{21} & 1 - (1 - \epsilon)F_{22} & -(1 - \epsilon)F_{23} & -(1 - \epsilon)F_{24} & -(1 - \epsilon)F_{25} & -(1 - \epsilon)F_{26} & -(1 - \epsilon)F_{27} \\ -(1 - \epsilon)F_{31} & -(1 - \epsilon)F_{32} & 1 - (1 - \epsilon)F_{33} & -(1 - \epsilon)F_{34} & -(1 - \epsilon)F_{35} & -(1 - \epsilon)F_{36} & -(1 - \epsilon)F_{37} \\ -(1 - \epsilon)F_{41} & -(1 - \epsilon)F_{42} & -(1 - \epsilon)F_{43} & 1 - (1 - \epsilon)F_{44} & -(1 - \epsilon)F_{45} & -(1 - \epsilon)F_{46} & -(1 - \epsilon)F_{47} \\ -(1 - \epsilon)F_{51} & -(1 - \epsilon)F_{52} & -(1 - \epsilon)F_{53} & -(1 - \epsilon)F_{54} & 1 - (1 - \epsilon)F_{55} & -(1 - \epsilon)F_{56} & -(1 - \epsilon)F_{57} \\ -(1 - \epsilon)F_{61} & -(1 - \epsilon)F_{62} & -(1 - \epsilon)F_{63} & -(1 - \epsilon)F_{64} & -(1 - \epsilon)F_{65} & 1 - (1 - \epsilon)F_{66} & -(1 - \epsilon)F_{67} \\ -(1 - \epsilon)F_{71} & -(1 - \epsilon)F_{72} & -(1 - \epsilon)F_{73} & -(1 - \epsilon)F_{74} & -(1 - \epsilon)F_{75} & -(1 - \epsilon)F_{76} & 1 - (1 - \epsilon)F_{77} \end{array} \right] & \cdot \left[ \begin{array}{c} J_1 \\ J_2 \\ J_3 \\ J_4 \\ J_5 \\ J_6 \\ J_7 \end{array} \right] & = \left[ \begin{array}{ccccccc} \epsilon \sigma T_{14} \\ \epsilon \sigma T_{24} \\ \epsilon \sigma T_{34} \\ \epsilon \sigma T_{44} \\ \epsilon \sigma T_{54} \\ \epsilon \sigma T_{64} \\ \epsilon \sigma T_{74} \end{array} \right] \end{align*} \]

Es folgt eine Fallunterscheidung mit und ohne externe solare Wärmequelle. Dabei wird angenommen, dass die Heizung eine Oberflächentemperatur von 80°C aufweist. Diese Temperatur liegt am unteren Rand der Oberflächentemperaturen von IR-Strahlungsheizkörpern. Die Wände im U-CUBE sollen unter der strahlungsdominierten Beheizung eine Oberflächentemperatur von 20°C haben, d.h. dass alle Oberflächen außer der Heizung die selbe Temperatur von 20°C haben. Diese Annahme wird nur getroffen, um die Rechnung übersichtlicher zu gestalten (Man könnte genauso gut die durch Konvektionsströme variierenden Oberflächentemperaturen berücksichtigen).Wenn tagsüber die Sonne scheint, wird die bestrahlte Wand erwärmt. Da die U-CUBES keine Fenster haben, wirkt sich der solare Eintrag lediglich über eine Erhöhung der Temperatur der Innenoberfläche der von außen bestrahlten, massiven Wand aus.

Messungen haben ergeben, dass mit einer Temperaturerhöhung von bis zu 2K an der Innenseite der bestrahlten Wand gerechnet werden kann.

Darum wird hier im zweiten Fall davon ausgegangen, dass die bestrahlte Wand (A3) eine Oberflächentemperatur von 22°C hat. Alle Oberflächen bekommen in dieser Simulation eine Emissivität von 0,9. Damit kann das Gleichungssystem folgendermaßen geschrieben werden:

\[ \left[ \begin{array}{cccccc} 1 & 0 & -0.024 & -0.019 & -0.019 & -0.019 \\ 0 & 1 & -0.02 & -0.02 & -0.02 & -0.02 \\ -0.00117 & -0.01883 & 1 & -0.02 & -0.02 & -0.02 \\ -0.001 & -0.019 & -0.02 & 1 & -0.02 & -0.02 \\ -0.001 & -0.019 & -0.02 & -0.02 & 1 & -0.02 \\ -0.001 & -0.019 & -0.02 & -0.02 & -0.02 & 1 \end{array} \right] \cdot \left[ \begin{array}{c} J_1 \\ J_2 \\ J_3 \\ J_4 \\ J_5 \\ J_6 \\ J_7 \end{array} \right] = \left[ \begin{array}{ccccccc} 793.71 \\ 376.86 \\ 376.86 \\ 376.86 \\ 376.86 \\ 376.86 \\ 376.86 \end{array} \right] \]

Die Helligkeiten werden nun berechnet, indem die invertierte Koeffizientenmatrix mit dem Lösungsvektor multipliziert wird. Dabei ergeben sich für die beiden konkreten Beispiele die folgenden Helligkeiten:

\[ \begin{align*} J_{ohneSonnenne} = \left[ \begin{array}{ccccccc} 835,63 \\ 418,79 \\ 419,26 \\ 419,26 \\ 419,26 \\ 419,26 \\ 419,26 \end{array} \right] \frac{W}{m^2} \qquad J_{mitSonnenne} = \left[ \begin{array}{ccccccc} 835,90 \\ 419,01 \\ 429,68 \\ 419,42 \\ 419,42 \\ 419,42 \\ 419,42 \end{array} \right] \frac{W}{m^2} \end{align*} \]

Man erkennt die Auswirkung des solaren Eintrags an den erhöhten thermischen Helligkeiten.

Der von der Heizung in den beiden Fällen abgestrahlte Wärmestrom Q̇₁teilt sich entsprechend der elektri¬schen Analogie in die Wärmeströme Q̇_1j auf.

Dabei gilt:

\[ \dot{Q}_{1j} = ( J_1 - J_j ) \cdot F_{1j} \cdot A_1 \\\ \\\ \begin{align*} \dot{Q}_1 &= \sum \dot{Q}_{1j} &= \sum (J_1 - J_j) \cdot F_{1j} \cdot A_1 \end{align*} \]

Wandflächen mit gleicher Helligkeitsdifferenz als treibende Potentialdifferenz des Wärmestroms können zusammengenommen werden.

Für die Strahlungsleistung der Heizung ohne solaren Eintrag ergibt sich damit:

\[ \dot{Q}_1 = 0.36 \cdot \left( (835.63 - 419.26) \cdot 0.24 + (835.63 - 419.19) \cdot 0.76 \right) = 149.91 \, \text{W} \]

Für die Strahlungsleistung der Heizung mit solarem Eintrag ergibt sich:

\[ \dot{Q}_{1s} = 0.36 \cdot \left( (835.90 - 429.68) \cdot 0.24 + (835.90 - 419.42) \cdot 0.76 \right) = 149.05 \, \text{W} \]

Mit dem solaren Energieeintrag ist eine Veränderung der Strahlungsleistung der Heizung verbunden, die deutlich unterhalb von einem Prozent der Strahlungsleistung liegt.

Da die Messgenauigkeit der Strahlungsmessung ebenfalls nur im Bereich von ca. 1 Prozent liegt, kann der solare Eintrag bei U-CUBE vernachlässigt werden. Die Messung der Strahlungseffizienz wird durch äußere Wärmequellen nicht beeinflusst und repräsentiert die tatsächliche Strahlungsleistung im Rahmen der Messgenauigkeit.

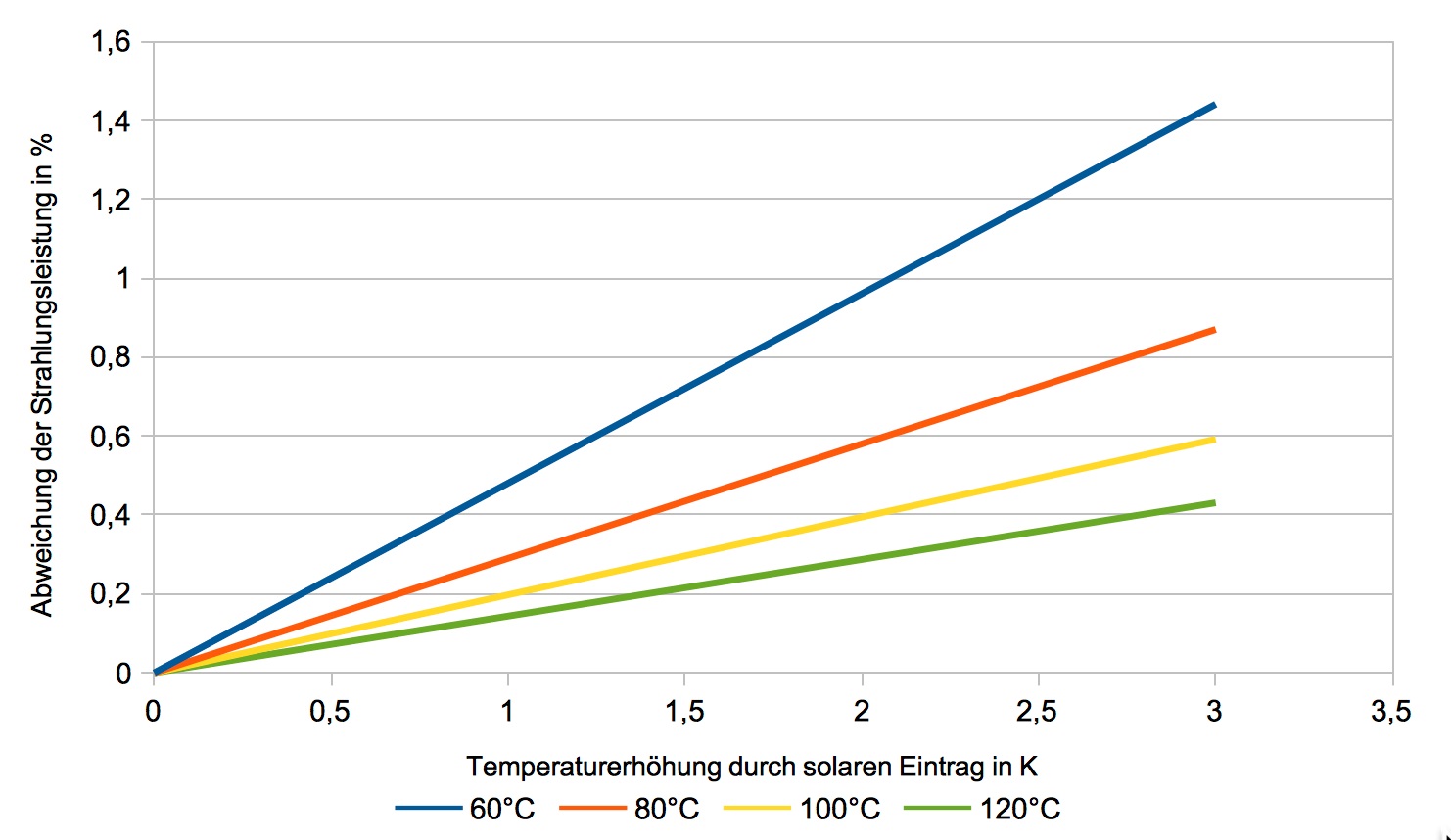
Die obige Abbildung zeigt die zu erwartende Abweichung der Strahlungsleistungsmessung der Heizung bei einer zusätzlichen externen Energiequelle (Sonne) in Abhängigkeit von der erzeugten Temperaturerhöhung der Innenoberfläche einer Wand bei verschiedenen Heizungsoberflächentemperaturen. Die gemessenen Temperaturunterschiede durch solare Erwärmung betrugen in der Heizperiode 2017/2018 maximal 2K bei einer 10cm dicken Massivholzwand. Bei massiverem Wandaufbau fällt die Temperaturdifferenz kleiner aus. Zusammenfassend kann gesagt werden, dass insbesondere bei IR-Strahlungsheizungen, deren Oberflächentemperatur 60 °C überschreitet, der solare Energieeintrag bei der Beurteilung der Strahlungsleistung der Heizung vernachlässigt werden kann.

Die U-CUBE Messmethode für die Strahlungstemperatur

Während der externe Energieeintrag in die Kuben für die Beurteilung der Strahlungsleistung der Heizung keine signifikante Rolle spielt, ist er doch für die Behaglichkeitsinterpretation des Strahlungsfeldes interessant. Durch die Strahlungsmessung mit richtungsauflösenden Strahlungssensoren kann ein solarer Eintrag durch Veränderungen der Tag/Nacht-Verteilungen gemessen und quantifiziert werden. Ebenso kann die Strahlungstemperatur in Raummitte und die Strahlungsasymmetrie quantitativ erfasst werden. Darum soll nun näher beschrieben werden, wie die Messmethode funktioniert.

Es kommen 6 IR-Strahlungssensoren mit einem Blickwinkel (FOV) von 90° zum Einsatz, die in Raummitte platziert werden. Jeder Sensor erfasst somit einen Kreisausschnitt mit einem Radius, der seinem Abstand r von der Wand entspricht. Das ist in der Regel ein Kreis mit einem Durchmesser, der der Wandbreite der quadratischen Wand entspricht. Die Sensoren messen die mittleren Helligkeiten J*_i ihres FOV. Üblicherweise werden Strahlungssensoren dazu eingesetzt, die Oberflächentemperaturen ihres FOV zu bestimmen. Dazu muss allerdings die Emissivität dieser Oberfläche zuvor sehr genau ermittelt werden.

Bei U-CUBE werden die Sensoren als Helligkeitssensoren betrieben und liefern präzise virtuelle Temperaturen der Oberflächen T_ji, die mit dem Stefan-Boltzmann-Gesetz in die gemessenen Helligkeiten J_i umgerechnet werden können (In Wahrheit misst der Sensor die Helligkeit als Strahlungsleistung und berechnet daraus mit einer voreingestellten Emissivität eine Temperatur - wir kehren das Prinzip um und vermeiden den Umrechnungsfehler). Der Sensor S₁₂ erfasst eine Kreisfläche auf der Wand A2, die die Heizfläche A1 beinhaltet. Auf dieser Fläche A12 wird eine mittlere Helligkeit J^*₁₂ gemessen.

\[ J^*_{12} = \frac{J_1 \cdot A_1 + J_2 \cdot (\pi \cdot r^2 - A_1)}{\pi \cdot r^2} \]

Der Sensor S₁₂ misst somit eine virtuelle Temperatur der Heizungsumgebung:

\[ T_{12}^* = \sqrt{\sqrt{\frac{J_{12}^*}{\sigma}}} \]

Für das konkrete Beispiel der quadratischen Heizfläche in Wandmitte, das z.B. bei einer Deckenheizung Anwendung findet, würden die IR-Sensoren die folgenden Temperaturwerte T_i liefern (Abstand des Sensors S₁₂ von der Wand A2 sei 1,3m):

\[ T = \left[ \begin{array}{ccccc} T_{12}^* \\ T_3 \\ T_4 \\ T_5 \\ T_6 \\ T_7 \end{array} \right] = \left[ \begin{array}{ccccc} 24,834 \\ 20,092 \\ 20,080 \\ 20,080 \\ 20,080 \\ 20,080 \end{array} \right] ^\circ \mathrm{C} \]

Die virtuellen Temperaturen liegen über den tatsächlichen Oberflächentemperaturen, da bei der Helligkeit der reflektierte Strahlungsanteil mit berücksichtigt wird. Die dargestellte Genauigkeit der Temperaturmessung wird in der Praxis nicht erreicht und dient hier nur der Illustration der Methodik. Aus den gemessenen virtuellen Temperaturen ergeben sich die gemessenen Helligkeiten:

\[ J = \left[ \begin{array}{ccccc} J_{12}^* \\ J_3 \\ J_4 \\ J_5 \\ J_6 \\ J_7 \end{array} \right] = \left[ \begin{array}{ccccc} 447.05 \\ 419.26 \\ 419.19 \\ 419.19 \\ 419.19 \\ 419.19 \end{array} \right] \frac{W}{m^2} \]

Die Helligkeiten treiben als Potentialdifferenz einen Wärmestrom von der virtuellen Heizfläche A12 zu den 5 umliegenden Wänden. Der jeweilige Teilstrom wird mit den Sichtfaktoren gewichtet. Es werden aber nicht die Sichtfaktoren der virtuellen Kreisfläche, sondern die realen Sichtfaktoren der Heizfläche verwendet, da der Wärmestrom ja von der Heizung kommt (siehe obige Einstrahlzahlenmatrix). Damit ergibt sich:

\[ \dot{Q}_1 = \pi \cdot 1.32 \cdot \left( (447.05 - 419.26) \cdot 0.24 + (447.05 - 419.19) \cdot 0.76 \right) = 147.8 \, \text{W} \]

Die Messung der Heizleistung weist eine Abweichung durch Rundungsfehler von 1,4% auf. Dieser Fehler wird in der Praxis reduziert, indem ein siebter IR-Sensor dichter an der Heizung platziert wird. Dadurch lässt sich der Messfehler auf ca. 1% minimieren. Der Vorteil der U-CUBE Methode zur Messung der Strahlungsleistung besteht neben der Genauigkeit darin, dass weder die Form, noch die Emissivität oder die Oberflächentemperatur der Heizung, noch die Emissivitäten und Oberflächentemperaturen der Wände bekannt sein müssen. Damit ist die Methode sehr schnell und unkompliziert.

Wir verwenden für unsere Messungen Melexis MLX90614Dxx Sensoren für medizinische Anwendungen mit einer erhöhten Genauigkeit im Temperaturbereich von 16°C bis 40°C. Die erreichbare Genauigkeit für Strahlungstemperaturmessungen beträgt damit ± 0,2K.